2022-08-24 10:17:09 来源： web开发网
二、等比数列前n项和
求等比数列的前n项和的过程中体现了两种高中数学的思想：
1)方程思想
等比数列求和公式中有一个知三求二问题，这就是方程思想的体现。
2)分类讨论的思想
在进行等比数列求和的过程中，由于等比数列的q是否为1，严重影响了等比数列求和的公式选取，这就用到了分类讨论思想。
三、等比数列求和性质
已知Sn为等比数列的前n项和，可以得到下述：
这就是等比数列前n想和的性质，对上述公式分析就是从第一项开始选取n项化为片段，这种片段之间仍然成等比数列。
四、求解提示
在等比数列前n项和求解过程中，除了需要注意：
1)公比是否为1
2)序号之间的联系，从而发现解题的方法。
高中数列是非常重要的考点，关于数列的考题虽然表面看去变化多样，但看其本质，可归结为两大类：求一个数列的通项an,求一个数列的前n项和。这篇文章就针对等差和等比数列求和公式给出推导和证明过程。
1等比数列前n项和公式
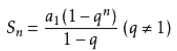
公式中a1为数列首项，q为等比数列的公比，Sn为前n项和。
2等差数列等比数列前n项和公式
3等比数列求通项方法
高考填报志愿时，杨凌职业技术学院招生计划是广大考生和家长朋友们十分
高考填报志愿时，西安工商学院招生计划是广大考生和家长朋友们十分关心
2023山东航空服务高考分数线已经公布，以下是大学生必备网为大家整理的
高考填报志愿时，湖南女子学院招生计划是广大考生和家长朋友们十分关心
2023贵州高考志愿有本科提前批、本科第一批、本科第二批、本科国家专项
